Suslin set

See also Suslin line for an entirely different concept in set theory, and Suslin space for topological spaces.

The concept of a Suslin set was first used by Mikhail Yakovlevich Suslin when he was researching the properties of projections of Borel sets in 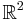$\R^2$ onto the real axis. Lebesgue believed he had proved that such a projection was also a Borel set, but an error was spotted by Suslin.

Suslin sets have since been used in various areas of mathematics such as potential theory, measure theory and the study of fractals.

There is some variation in the ways in which Suslin sets are defined in mathematical literature. In this article we follow what is probably the most common definition.

Definition

In a metric space 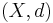$(X,d)$ , the Suslin sets are the sets of the form

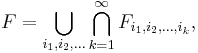
$F = \bigcup_{i_1,i_2,\dots}\bigcap_{k=1}^\infty F_{i_1,i_2,\dots,i_k},$

where 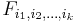$F_{i_1,i_2,\dots,i_k}$ is a closed set in X for each finite sequence 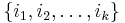$\{ i_1, i_2, \dots, i_k\}$ of positive integers.

Properties of Suslin sets

Every Borel set is a Suslin set.
The collection of all Suslin sets is closed under countable unions and countable intersection.
Not all Suslin sets are Borel sets (in non-trivial metric spaces such as $\R^n$ ).
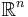If A is a subset of a Polish space then A is a Suslin set if and only if it is an analytic set.
In a Polish space, any Suslin set is universally measurable.

References

J. L. Doob. Classical Potential Theory and Its Probabilistic Counterpart, Springer-Verlag, Berlin Heidelberg New York, ISBN 3-540-41206-9.
R. M. Dudley. Real Analysis and Probability, Chapman & Hall, 1989.
C. A. Rogers. Hausdorff Measures, Cambridge University Press, 1998.
K. J. Falconer. The Geometry of Fractal Sets, Cambridge University Press, 1985.